此篇目为游戏感想
在游戏《Turing Complete》中,我遇到了如下关卡,令我印象深刻:
相反数
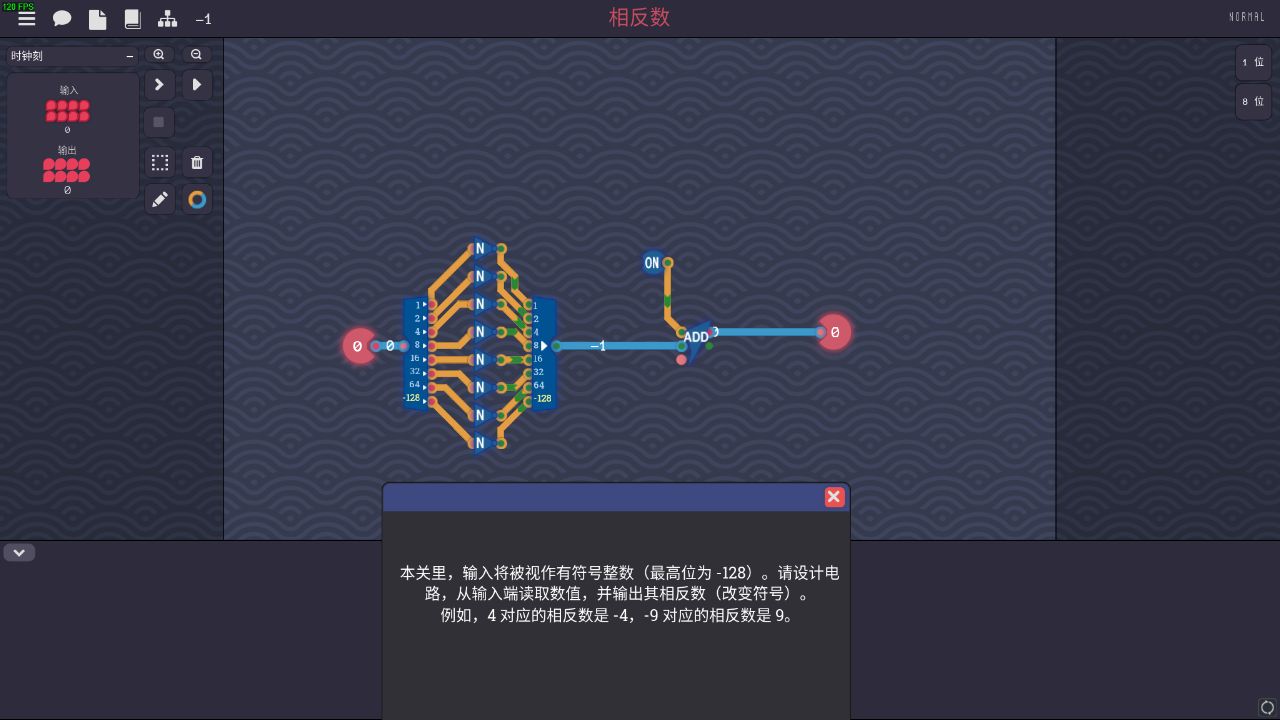
做到相反数,一个二进制的相反数其实就是它的补码。为了区分正负,二进制数用最高位来表示符号,1为负,0为正。用8位二进制数举例,0000 0001=1,1000 0001=-1。
十进制中相反数直接在数字前加负号就可,那么二进制的相反数怎么求呢?不管是十进制还是二进制,相反数的意义都是指:该数+该数的相反数=0。比如 0000 0011 + 它的相反数 = 0000 0000 ,那么 0000 0011的相反数=0000 0000 - 0000 0011 = 1111 1101,直观上理解就是一个数的相反数=对该数按位取反再加1。
下面从理论推导一下:对于某个不为0的二进制数来说,该数+它的相反数=0000 0000,那么该结果一定是由于进位溢出造成的(用二进制相加看,不要用十进制看),相当于1111 1111 + 0000 0001 = 0000 0000,用未溢出的值代替0000 0000,即 该数 + 它的相反数=1111 1111 + 0000 0001,⟶ 它的相反数 = 1111 1111 - 该数 +0000 0001,1111 1111 - 该数 就相当于对该数按位取反,所以二进制数的相反数就是对其按位取反加1。
我们自己理解的话0000 0011=3,它的相反数为-3=1000 0011,但0000 0011 + 1000 0011 != 0000 0000,所以计算机就引入了补码,相当于上面的相反数的表示。将人容易理解的二进制称为原码,计算机实际使用时用的是补码。正数的补码就是自己,负数的补码为按位取反加1。
对于1000 0011来说,若其为原码,则表示-3;若其为补码,则表示(-1)2^7 + 12^1 + 1*2^0 = -125。
计数器
这题其实不算难,但是我楞了很久。
题目:

如下设计:
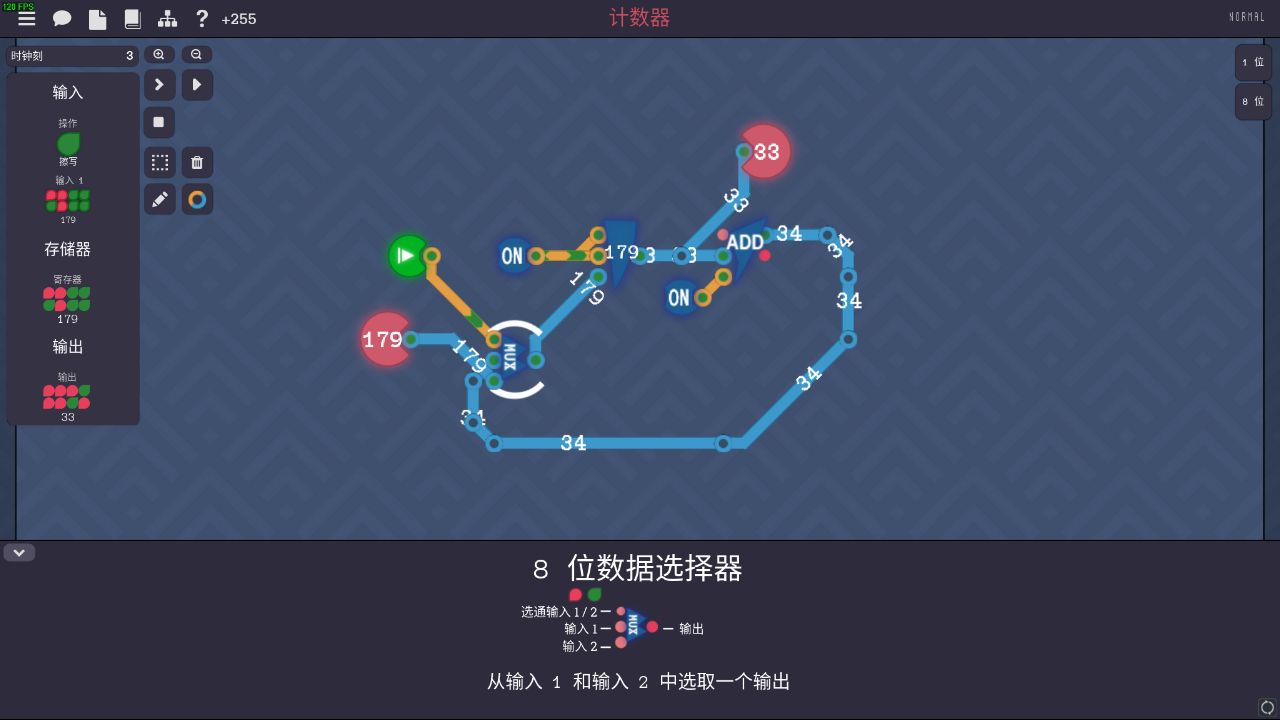
寄存器会始终把数据存储并输出,并且直接输出到输出端。到下一段后,因为有ADD在,会+1(高电平就是1),然后再输出出来,重新写入到寄存器。左侧的高电平时为了始终启用寄存器的读取和写入功能。这样,在不覆盖的状态下,寄存器会每刻都+1。只需要用到一个选通器,选择让哪个数据覆盖到寄存器即可。
锁存器等
这个是我在游戏的提示里面看到的,由循环依赖衍生而出。与非门锁存器。游戏里面一般不允许出现循环依赖,但它在现实世界中是广泛存在的。
恶补触发器的原理,电平、脉冲和边缘触发器的不同等(参考数电课本)。然后对知识进行一个接轨,把所以已知的内容和生活的认知形成闭环。感觉整个体系对于现在态和未来态要有一定的敏感性,就是不能混淆,然后看时序图得认真看哪个是CLK。正常看时序报告即可,也算是把之前移位寄存器的课给补上了。
忽然就想起来这种概念我第一次接触是在哪里了,是mc的记忆电路。